Kerne als Teilchengitter
Atomkerne bestehen aus leichten Teilchen (vor allem geladene Pionen, Kaonen und selten auch Myonen), die sich zu einem möglichst symmetrischen Teilchengitter formieren. Da Protonen und Neutronen ebenfalls aus diesen Teilchen bestehen, können sie einerseits von instabilen Kernen emittiert werden, andererseits liegen Protonen und Neutronen im Kern nicht als diskrete Teilchen vor, sondern verschmelzen zur einheitlichen Kernmaterie. Die strukturelle Übereinstimmung von Teilchen und Kernen ist die Ursache, dass bei Kernzertümmerungen, wenn Kerne also explosionsartig zerstörtwerden, viele leichte und schwere Teilchen beobachtet werden.
10.1 Ein Musterbeispiel der Symmetrie - der Kern des Kohlenstoff-12
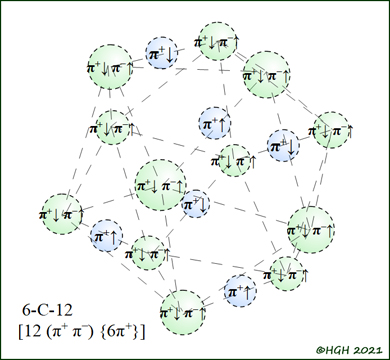
Die Abbildung zeigt ein Modell des Kerns 6-C-12. In den Ikosaeder der 12 Masseteilchen können sich die 6 bindenden Teilchen bei vollständiger Spinpaarung ausgezeichnet einordnen. Dieser Kern fällt in Abb. 9.1 (Verlauf der Kernbindungsenerie) durch einen besonders hohen Wert auf. Kohlenstoff 6-C-12 dient als Bremssubstanz (Moderator) und Abschirmung für Neutronen in Spaltreaktoren. Den permanenten Angriff durch die reaktiven Neutronen kann nur ein geschlossener (inerter) Kern dauerhaft überstehen. Bekannt ist, dass der Nachbarkern 5-B-11 mit seinem defizitären Kerngitter als "Neutronen-Fresser" in Form von Regelstäben die Kettenreaktion in Kernreaktore sofort unterbricht.
Die hohe Stabilität des Kerns 6-12 wird in Darstellungen und Theorien meistens negiert. Er passt nicht in das von den Theoretikern konstruierte Modell der "Kernschalen". "Kernschalen" lassen sich nur insofern nachvollziehen, dass es Teilchengitter mit besonders hohen Symmetriewerten gibt. In einigen Fällen stimmen hochsymmetrische Teilchengitter und vermutete Kernschalen überein. Beispielsweise betrifft das den schon beschriebenen Kern 2-He-4 und die Kerne 8-O-16 und 82-Pb-208. Auch dies ist ein schönes Beispiel, wie die Realität mit theoretischen Parallelen zwar beschrieben wird, ohne dass die Realität ursächlich erkannt wurde.
10.2 Die Kerngitter leichter stabiler Kerne
Abb. 10.2: Zusammenhang zwischen Kerngeometrie und Kernbindungsenergie
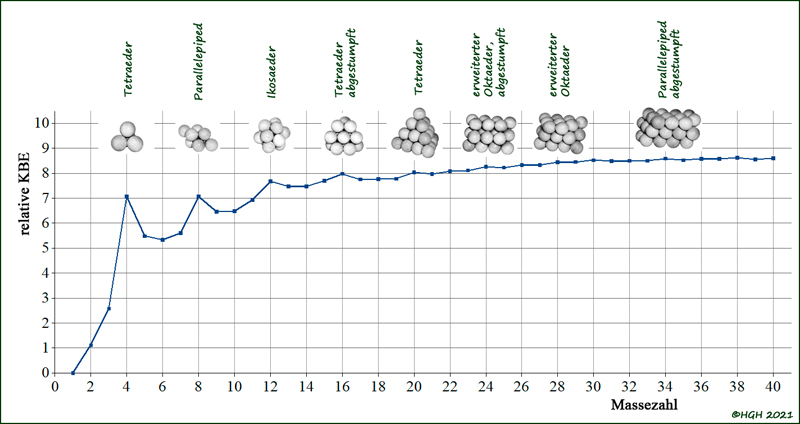
Für jeden besonders stabilen Kern mit hoher Bindungsenergie kann ein Teilchengitter gefunden werden, welches sich durch hohe Symmetrie und Geschlossenheit auszeichnet. Dabei muss berücksichtigt werden, dass innerhalb des Masseteilchengitters, wie es in der Abb. 10.2 dargestellt ist, auch das Gitter aus bindenden Teilchen symmetrisch perfekt integriert sein muss. So besitzt Kern 10 trotz seines tetraedrischen Gitters keinen lokalen Maximalwert an Bindungsenergie, weil das Bindungsgitter mit 5 Teilchen keine Spinpaarung erlaubt: Der Spin des Kerns ist +3.
10.3 Generelle Aussagen zur Kern-Symmetrie
Die leichten Atomkerne bis Massezahl A=16 müssen in vielen Fällen als ein 'unausgegorener Haufen von Halbwüchsigen' bezeichnet werden, weil sie sehr uneinheitlich sind. Das Erreichen einer hinreichenden Symmetrie ist bei ihnen oft nicht möglich, weil ein einzelnes Masseteilchen große Auswirkung auf Symmetrie und Stabilität eines Kerns hat. Bei den schweren Kernen ist der Einfluss eines einzelnes Masseteilchens sehr viel geringer. Es stehen außerdem mehr Möglichkeiten einer hinreichend stabilen Anordnung zur Verfügung. Die nachfolgenden Abbildungen demonstrieren die symmetrische Ausprägung schwererer Kerne. Die Beschreibung jedes einzelnen Kerns ist hier allerdings nicht möglich.
Beispielhafte Struktur des Kerns 28-Ni-62
Die häufigste Form der Atomkerne zeigt beispielhaft der Kern 28-62. Dieser Kern besitzt die höchste Bindungsenergie je Masseteilchen. Geometrisch gesehen sind diese Kernkörperchen von Parallelogrammen begrenzte und an ihren Spitzen meistens abgestumpfte Parallelepipede. Diese Kernform erklärt selbstredend die Quadrupol-Momente der Atomkerne, die mit dem 'Tröpchenmodell' oder von im Kern herumrasenden Teilchen (Fermigasmodell) nicht vereinbar sind. Die derzeit existierenden widersprüchlichen Kernmodelle können durch ein einziges Modell ersetzt werden, welches hier als "Kerngittermodell" bezeichnet wird.